matlab与FPGA无线通信、FPGA数字信号处理系列(2)——Vivado调用IP核设计FIR滤波器
本文共 2005 字,大约阅读时间需要 6 分钟。
本讲在Vivado调用FIR滤波器的IP核,使用 中的 matlab 滤波器参数设计 FIR 滤波器,下两讲使用 和 ,结合 FIR 滤波器搭建一个信号产生及滤波的系统,并编写 testbench 进行仿真分析,预计 、 开始编写 verilog 代码设计 FIR 滤波器,不再调用 IP 核。
本例使用 Vivado 2018.2 调用 IP 核实现 FIR 滤波器,使用中的matlab的fdatool工具箱导出的滤波器参数(FIR_BPF_99_1_5M.coe文件)。

1.新建工程
(1)Create Project -> RTL Project,一直Next直到选择器件,选择自己使用的器件; (2)新建原理图文件,Create Block Design; (3)将上一讲中从 MATLAB 中导出的FIR_BPF_99_1_5M.coe文件放在新建工程后的工程目录下;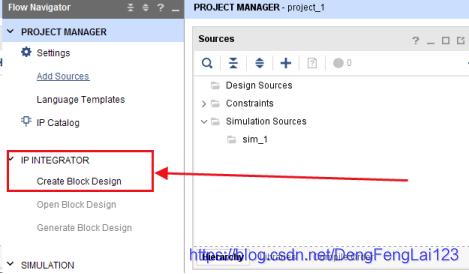
2.添加IP核
(1) 加入FIR的IP核,在新建的原理图文件design_1中点击 1 处的加号,会弹出对话框,在2处输入 fir 即可(不区分大小写),双击 3 处的 ”FIR Complier”; (2) 原理图中出现FIR的原理图,双击该IP核;
(2) 原理图中出现FIR的原理图,双击该IP核; 
3.配置FIR滤波器IP核
(1)在第一页Filter Options中,红色框内可以配置滤波器的系数来自 .COE 文件(COE File)或者来自向量形式(Vector),此处选择 “COE File”;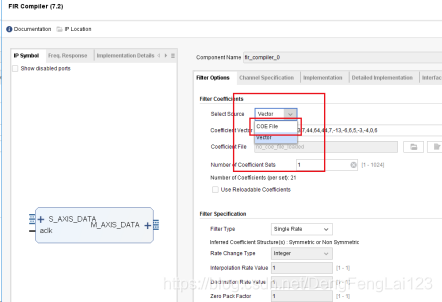 (2)1处变为COE File后,点击 2 处加载/导入滤波器的系数文件,弹出文件选择框,选择 3 处的 FIR_BPF_99_1_5M.coe(中从 MATLAB 中导出的文件,新建工程后将其放在工程目录下),点击 4 处的确定,成功加载。
(2)1处变为COE File后,点击 2 处加载/导入滤波器的系数文件,弹出文件选择框,选择 3 处的 FIR_BPF_99_1_5M.coe(中从 MATLAB 中导出的文件,新建工程后将其放在工程目录下),点击 4 处的确定,成功加载。  加载成功后可以看到,1处显示出文件的路径;2处默认为1,表示有几路滤波通道,此处选择 1 路;3处的数据是100,无法更改,表示的是从刚刚加载的 .coe 文件中读取到 100 个滤波器系数;
加载成功后可以看到,1处显示出文件的路径;2处默认为1,表示有几路滤波通道,此处选择 1 路;3处的数据是100,无法更改,表示的是从刚刚加载的 .coe 文件中读取到 100 个滤波器系数; 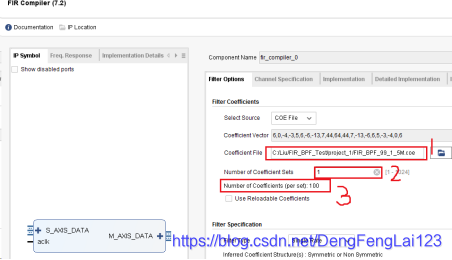 (3)滤波器配置-2 点击 1 处配置滤波器的第 2 页,主要配置 2 处的系统时钟和数据采样时钟,在上一讲中设置 matlab 滤波器参数时是 32 MHz采样频率,所以此处选择输入采样时钟为 32 MHz,为了方便起见,此处设置系统时钟为 32 MHz(实际工作中系统时钟不是这个频率的,可以通过PLL等获得 32 MHz,此处我们只做仿真,系统时钟可以通过 testbench 任意设定);
(3)滤波器配置-2 点击 1 处配置滤波器的第 2 页,主要配置 2 处的系统时钟和数据采样时钟,在上一讲中设置 matlab 滤波器参数时是 32 MHz采样频率,所以此处选择输入采样时钟为 32 MHz,为了方便起见,此处设置系统时钟为 32 MHz(实际工作中系统时钟不是这个频率的,可以通过PLL等获得 32 MHz,此处我们只做仿真,系统时钟可以通过 testbench 任意设定); 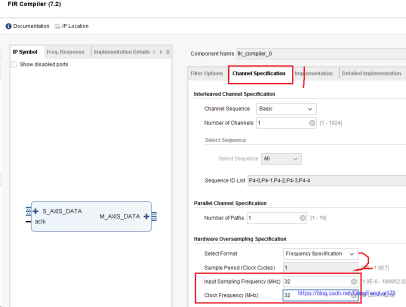 (4)滤波器配置-3 点击 1 处配置第 3 页;2 处设置滤波器系数的格式,有符号数signed,整数类型,位宽为 16 位(在上一讲中是将滤波器系数进行 16 位量化后导出);3处选择滤波器结构,上一将中设计的滤波器是对称结构,选择Symmetric;4处配置输入数据的格式,此处保持默认,输入有符号数,16位宽度,,如果输入的要滤波的数据不是该配置,可以点击5处的正方形,点击之后对应的方框有灰色变成白色,可以进行修改里面的参数;
(4)滤波器配置-3 点击 1 处配置第 3 页;2 处设置滤波器系数的格式,有符号数signed,整数类型,位宽为 16 位(在上一讲中是将滤波器系数进行 16 位量化后导出);3处选择滤波器结构,上一将中设计的滤波器是对称结构,选择Symmetric;4处配置输入数据的格式,此处保持默认,输入有符号数,16位宽度,,如果输入的要滤波的数据不是该配置,可以点击5处的正方形,点击之后对应的方框有灰色变成白色,可以进行修改里面的参数; 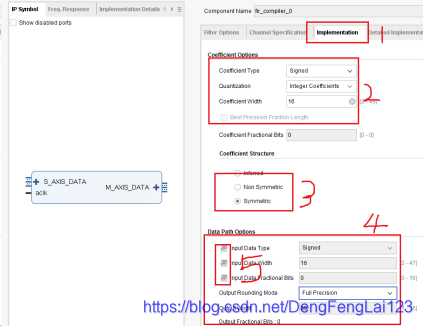 (5)其他保持默认,点击OK退出配置。
(5)其他保持默认,点击OK退出配置。 4.例化IP核
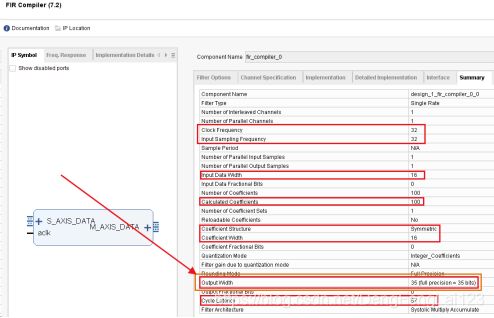
(1)熟悉输入输出端口 FIR的IP核直接给出了AXI-Stream形式的接口(一种符合AXIS-Stream总线协议的端口,此处不需要太关注该协议,用不到),点击两个“+”可以展开里面包含的端口,可以看到,共有: a.一个时钟端口 aclk,频率为 32 MHz; b.两个输入 s_axis_ddata_tdata[15:0]:16位的待滤波的输入数据,采样频率 32 MHz,每个时钟周期输入一个数据; s_axis_data_tvalid:输入数据有效标志位,该位为1时表示输入的数据有效,在AXI-Stream协议中,该位与前一级的相关的接口自动相连,自动判断是否有效,本例中直接向该引脚传入“1”,即输入数据一直有效; c.三个输出 s_axis_data_tready:指示是否准备好接收输入数据; m_axis_data_tdata[39:0]:滤波后的输出数据,40位位宽(实际上可以在IP配置时可以看到最后一页的总结里面箭头所指处表示输出数据的位宽为35位,但是此处是AXI-Stream接口,数据必须是8的整数倍,所以是40位,但是最高的几位没有实际含义)。 m_axis_data_tvalid:指示输出数据有效,有效输出时该位为1;
 (2)引出端口 右键单击选择 “Make External”,引出端口后点击箭头所指处,可以让软件检查是否有连线错误;
(2)引出端口 右键单击选择 “Make External”,引出端口后点击箭头所指处,可以让软件检查是否有连线错误;  (3)例化IP核 点击 1 处出现 2,右键单击 2 后先点击 3 生成 IP 核的硬件描述语言,完成 3 后再点击 4 调用 IP 核进行例化;
(3)例化IP核 点击 1 处出现 2,右键单击 2 后先点击 3 生成 IP 核的硬件描述语言,完成 3 后再点击 4 调用 IP 核进行例化;  (4)例化完成
(4)例化完成 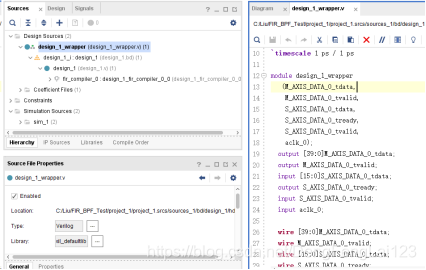
,结合FIR滤波器搭建一个信号产生及滤波的系统,并编写testbench进行仿真分析。
转载地址:http://rkte.baihongyu.com/
你可能感兴趣的文章
NIFI1.21.0通过Postgresql11的CDC逻辑复制槽实现_指定表或全表增量同步_实现指定整库同步_或指定数据表同步配置_04---大数据之Nifi工作笔记0056
查看>>
NIFI1.23.2_最新版_性能优化通用_技巧积累_使用NIFI表达式过滤表_随时更新---大数据之Nifi工作笔记0063
查看>>
NIFI从MySql中增量同步数据_通过Mysql的binlog功能_实时同步mysql数据_根据binlog实现数据实时delete同步_实际操作04---大数据之Nifi工作笔记0043
查看>>
NIFI从MySql中增量同步数据_通过Mysql的binlog功能_实时同步mysql数据_配置binlog_使用处理器抓取binlog数据_实际操作01---大数据之Nifi工作笔记0040
查看>>
NIFI从MySql中增量同步数据_通过Mysql的binlog功能_实时同步mysql数据_配置数据路由_实现数据插入数据到目标数据库_实际操作03---大数据之Nifi工作笔记0042
查看>>
NIFI从MySql中增量同步数据_通过Mysql的binlog功能_实时同步mysql数据_配置数据路由_生成插入Sql语句_实际操作02---大数据之Nifi工作笔记0041
查看>>
NIFI从MySql中离线读取数据再导入到MySql中_03_来吧用NIFI实现_数据分页获取功能---大数据之Nifi工作笔记0038
查看>>
NIFI从MySql中离线读取数据再导入到MySql中_不带分页处理_01_QueryDatabaseTable获取数据_原0036---大数据之Nifi工作笔记0064
查看>>
NIFI从MySql中离线读取数据再导入到MySql中_无分页功能_02_转换数据_分割数据_提取JSON数据_替换拼接SQL_添加分页---大数据之Nifi工作笔记0037
查看>>
NIFI从PostGresql中离线读取数据再导入到MySql中_带有数据分页获取功能_不带分页不能用_NIFI资料太少了---大数据之Nifi工作笔记0039
查看>>
nifi使用过程-常见问题-以及入门总结---大数据之Nifi工作笔记0012
查看>>
NIFI分页获取Mysql数据_导入到Hbase中_并可通过phoenix客户端查询_含金量很高的一篇_搞了好久_实际操作05---大数据之Nifi工作笔记0045
查看>>
NIFI分页获取Postgresql数据到Hbase中_实际操作---大数据之Nifi工作笔记0049
查看>>
NIFI同步MySql数据_到SqlServer_错误_驱动程序无法通过使用安全套接字层(SSL)加密与SQL Server_Navicat连接SqlServer---大数据之Nifi工作笔记0047
查看>>
NIFI同步MySql数据源数据_到原始库hbase_同时对数据进行实时分析处理_同步到清洗库_实际操作06---大数据之Nifi工作笔记0046
查看>>
Nifi同步过程中报错create_time字段找不到_实际目标表和源表中没有这个字段---大数据之Nifi工作笔记0066
查看>>
NIFI大数据进阶_FlowFile拓扑_对FlowFile内容和属性的修改删除添加_介绍和描述_以及实际操作---大数据之Nifi工作笔记0023
查看>>
NIFI大数据进阶_FlowFile生成器_GenerateFlowFile处理器_ReplaceText处理器_处理器介绍_处理过程说明---大数据之Nifi工作笔记0019
查看>>
NIFI大数据进阶_Json内容转换为Hive支持的文本格式_操作方法说明_01_EvaluteJsonPath处理器---大数据之Nifi工作笔记0031
查看>>
NIFI大数据进阶_Kafka使用相关说明_实际操作Kafka消费者处理器_来消费kafka数据---大数据之Nifi工作笔记0037
查看>>